Sep 01, 2024
Deparei-me recentemente com este post do Kadima Asset Management no Instagram
que falava sobre Fatos Estilizados. Este termo curioso é referente a um artigo do pesquisador Rama Cont que fala sobre propriedades estatísticas comuns a diversos ativos (e classes)
do mercado financeiro. O artigo lista 11 fatos estilizados, dos quais o último (dentre outros) me chamou à atenção, e aqui trago a tradução
trazida pelo post do Kadima Asset Management:
Assimetria nas escalas de tempo: Medidas de volatilidade em escalas de tempo mais amplas preveem a volatilidade em escalas de tempo mais curtas do que o contrário.
Este fato estilizado me chamou à atenção por ser um fato que podemos analisar de maneira relativamente simples (e, claro, empírica). Por causa
disso, resolvi "tirar isso a limpo" e fazer uma análise de se isso acontece ou não.
Primeiro passo: selecionando os ativos e coletando os dados
Resolvi testar o fato estilizado em ativos relacinados a índices de bolsas de valores, tesouro americano, commodities, ouro e Bitcoin. A lista
abrangendo os tickers de cada ativo e uma breve descrição deles pode ser conferida abaixo, montada pelo Perplexity (prompt aqui).
Aqui está a tabela em markdown, escrita em língua portuguesa, com os tickers solicitados:
| Ticker |
Descrição |
| ^GSPC |
Índice S&P 500, que representa as 500 maiores empresas de capital aberto dos EUA. É considerado um dos principais indicadores do mercado de ações americano. |
| ^BVSP |
Índice Bovespa, principal indicador de desempenho das ações negociadas na B3, a bolsa de valores brasileira. Reflete o comportamento das principais ações do mercado. |
| ^N225 |
Índice Nikkei 225, o principal índice da Bolsa de Valores de Tóquio. Representa as 225 maiores empresas japonesas listadas na primeira seção da bolsa. |
| ^FTSE |
FTSE 100, índice das 100 empresas com maior capitalização listadas na Bolsa de Londres. É um importante indicador do mercado de ações do Reino Unido. |
| ^GDAXI |
DAX 40, índice das 40 maiores empresas da Bolsa de Frankfurt. Representa o desempenho das principais companhias da economia alemã. |
| VWO |
ETF que busca acompanhar o desempenho de um índice que mede o retorno de ações de empresas localizadas em países de mercados emergentes. |
| AGG |
ETF que busca acompanhar o desempenho de um índice que mede o mercado total de títulos de renda fixa com grau de investimento e tributáveis nos EUA. |
| GLD |
ETF que busca refletir o desempenho do preço do ouro. Oferece aos investidores uma forma de investir em ouro sem a necessidade de armazenamento físico. |
| BTC-USD |
Par de negociação Bitcoin/Dólar americano. Bitcoin é a primeira e mais conhecida criptomoeda descentralizada do mundo. |
| TLT |
ETF que busca acompanhar o desempenho de um índice de títulos do Tesouro dos EUA com vencimento de 20 anos ou mais. |
| IEF |
ETF que busca acompanhar o desempenho de um índice de títulos do Tesouro dos EUA com vencimento entre 7 e 10 anos. |
| VTI |
ETF que busca acompanhar o desempenho de um índice que mede o retorno de investimento de todo o mercado de ações dos EUA. |
| DBC |
ETF que busca acompanhar o desempenho de um índice composto por contratos futuros de 14 commodities amplamente negociadas. |
Assim como na análise do portfolio de Ray Dalio, utilizei aqui a biblioteca Python
yfinance para baixar os dados OHLC (Open, High, Low, Close) do Yahoo Finance
referentes a cada ticker (a propósito, os códigos da análise estão disponíveis aqui). Feito isso, vamos ao nosso segundo passo:
Calculando e avaliando a volatilidade
Tradicionalmente, a volatidade é calculada como sendo o produto entre o desvio-padrão dos retornos de um ativos em um determinado período e
a raiz quadrada do período utilizado (para saber mais, veja este artigo da
Investopedia e este artigo do Seeking Alpha). E eu digo a você: eu utilizei
esta fórmula para calcular a volatilidade e fazer a análise. No entanto, ler o artigo de Rama Cont me fez "virar a chave" (finalmente) para um
detalhe que eu em parte já entendia mas que nunca me tinha caído a ficha até então. A grosso modo, dados de mercado financeiro
não seguem a distribuição normal (Gaussiana). Até aí tudo bem, quem mexe com finanças quantitativas já está careca de saber isso (inclusive
o artigo traz boas discussões sobre isso e inclusive o autor dedica boa parte do trabalho às "caudas longas"). E aí vem o pulo do gato: a forma
como o desvio-padrão tradicionamente calculado (confira esta lição da Penn State University
para saber mais) leva consideração que os dados justamente seguem a distribuição normal! E agora?
Eu tive então a seguinte ideia: ao invés de calcular a raiz-quadrada da variância (forma tradicional), e depois multiplicar pela raiz do
período, eu calculei a volatilidade como sendo a variação entre os "quantis" (ver este post para saber mais) de 95% e 5%, respectivamente, dos retornos no período. O cálculo de variação que usei foi basicamente o logartimo natural
da divisão entre o quantil de 95% e o de 5%.
A ideia por trás disso é: períodos com alta volatilidade irão apresentar intervalos de valores maiores para a divisão definida acima, enquanto
que períodos de volatilidade pequena irão assumir intervalor menores. O uso do logaritmo natural da divisão de valores inclusive é uma fórmula
tradicionalmente utilizada em finanças quantitativas para calcular retornos, uma vez que produz resultados simétricos (ex: o "log_natural(2/3)", tirando o sinal negativo, vai produzir o mesmo resultado que "log_natural(3/2)").
Para poder avaliar e comaparar o poder preditivo de volatilidades longas e curtas, eu decidi me utilizar de uma métrica muito comum em
Aprendizado de Máquina chamada Informação Mútua, que justamente traz uma forma
de quantificar o poder preditivo de uma característica sobre outra. Apesar dela ser mais comumente utilizada em problemas nos quais você quer
prever uma categoria, aqui a gente quer prever um número (para saber mais sobre, veja este link). Ainda assim, a biblioteca que usei para calcular ela tem um módulo adaptado para utilizá-la em problemas de "prever um número" (inclusive tem artigo que explica a diferença de uso). Observação final
importante: quanto maior for o valor da informação mútua, maior será o poder preditivo da volatilidade. Ou seja: nossa hipótese aqui é que volatilidades longas terão informação mútua maior do que volatilidades curtas.
Agora que sabemos como fiz para calcular a volatilidade, vamos ao nosso terceiro passo:
Fazendo os experimentos
Para testar se uma volatilidade longa consegue prever uma volatilidade curta melhor do que o inverso, a gente precisa elicitar três coisas:
quais períodos para volatilidades curtas utilizar, quais períodos para volatilidades longas utilizar, e para quais períodos futuros (quantos
dias frente) testar. E aqui entra o ponto talvez mais crucial e delicado da análise: no artigo de Rama Cont, ele chama de volatilidade curta
aquela com período de 30 minutos, e de longa aquela com período de 1 dia. Quando eu faço análises, eu utilizo normalmente dados diários
(que foi o caso aqui),e infelizmente só vim me atentar que há uma forma de baixar dados de intra-day usando o yfinance no momento da escrita
deste post, então deixo como dever de casa analisar intra-day versus diário. As volatilidades curtas e longas, assim como os períodos futuros para testar foram os seguintes:
- Volatilidade curtas: 2 dias, 3 dias, 5 dias e 10 dias
- Volatilidade longas: 1 mês, 3 meses, 6 meses e 1 ano (aqui eu considero "1 mês" como sendo 21 dias, e os demais períodos como sendo múltiplos de 21 dias. "1 ano" corresponderia a 252 dias (21 dias * 12 meses))
- Períodos futuros: 1 dia, 3 dias, 5 dias, 10 dias, 1 mês, 3 meses e 6 meses (na parte do mês, mesmo esquema de antes)
A ideia então foi calcular a informação mútua de todas as combinações possíveis dos valores acima e comparar os pares de volatilidades (por exemplo, a informação mútua de uma volatilidade de 1 mês sobre a volatilidade de 2 dias do dia seguinte, e vice-versa; a informação mútua da volatilidade de 1 mês sobre a volatilidade de 3 dias do dia seguinte, e vice-versa; e etc.). Detalhe importante, vamos ver isso para cada ativo da tabela da seção do Primeiro Passo.
Resultado do experimento (e discussão sobre)
Uma vez que a quantidade de combinações entre volatilidades e períodos futuros é bem alta, resolvi sumarizar os resultados em duas imagens. A primeira, a seguir, ilustra, para cada ticker de ativo da tabela do início deste post, as distribuições de Informação Mútua tanto para as Volatilidades Longas predizendo as Curtas (boxplots azuis) como para o inverso (boxplots laranjas), isso agregando todos os resultados para todos os períodos futuros.
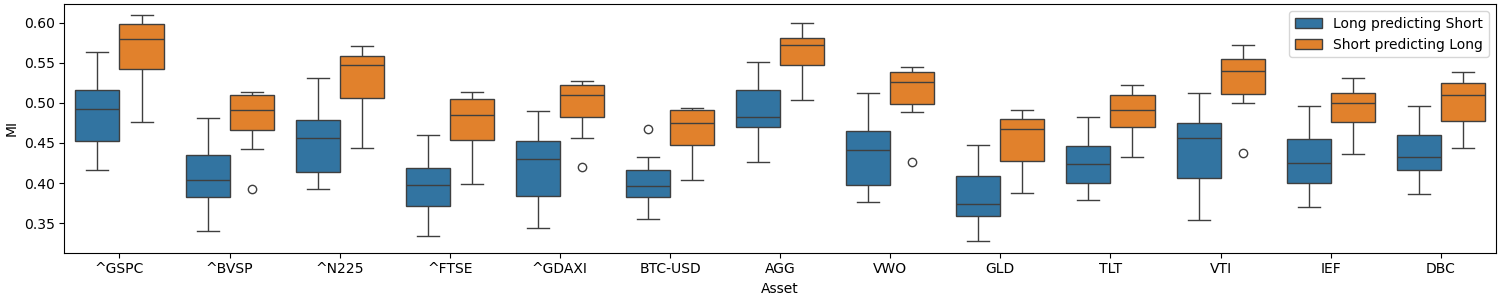
Figura 1 - Distribuição das Informações Mútuas obtidas para Volatilidades Longas predizendo Volatilidades Curtas e vice-versa
Conforme podemos observar, o resultado obtido é o "exato oposto" do que o fato estilizado diz: as volatilidades curtas possuem um poder preditivo melhor do que as longas! E pior: em ativos como o AGG e o VTI, a melhor Informação Mútua obtida para uma volatilidade longa bate no quartil de 25% da volatidade curta.
Aí a gente pode se perguntar: será que, para algum período específico, poderíamos ver volatilidades longas se saindo melhor que as curtas? Nisso, temos a segunda imagem, desta vez mostrando a média das Informações Mútuas dentre os períodos futuros para cada ativo:
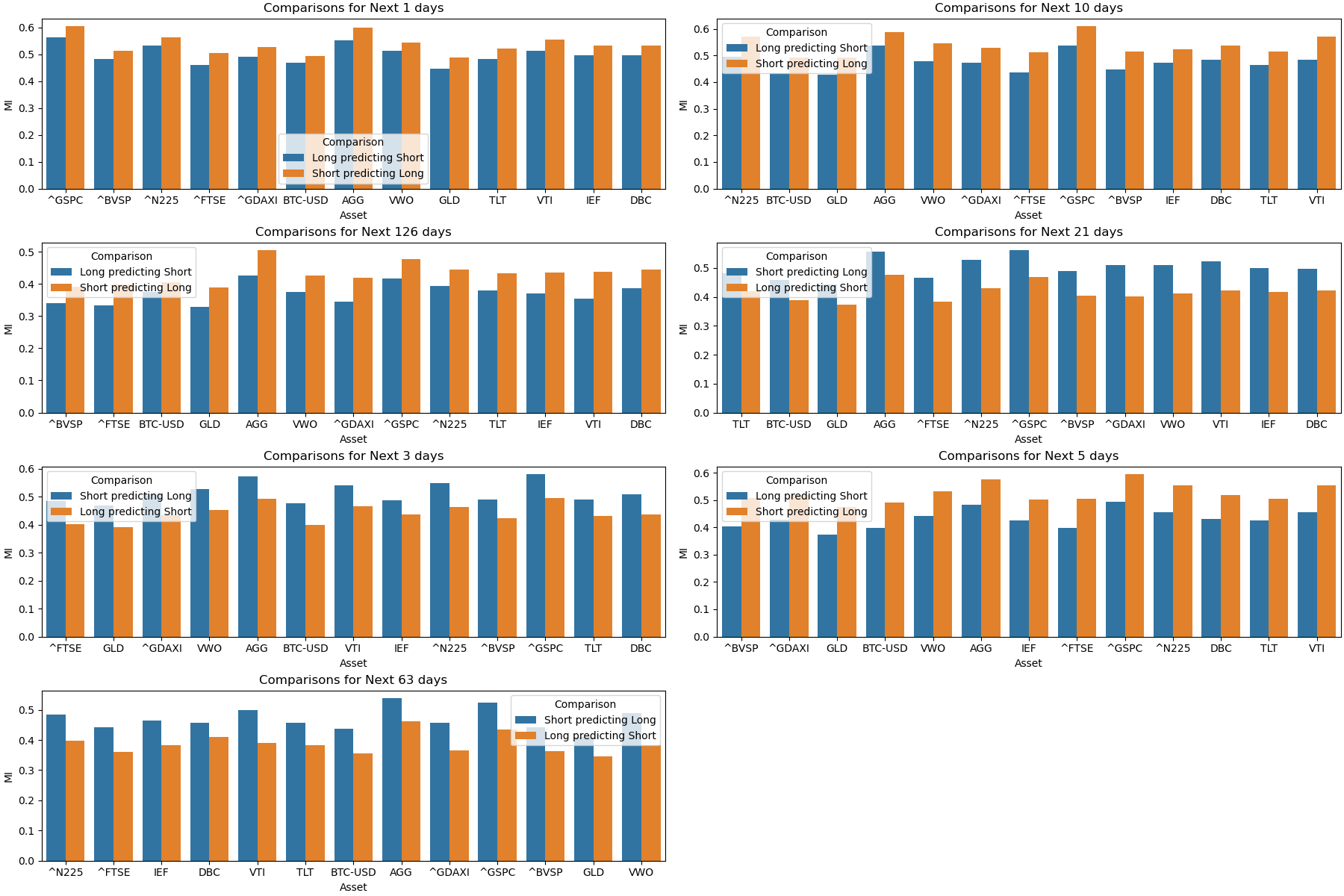
Figura 2 - Média das Informações Mútuas obtidas para Volatilidades Longas predizendo Volatilidades Curtas e vice-versa
E a resposta é clara: não. Em qualquer período futuro, a volatilidade curta tem poder preditivo melhor que a longa.
Nisso, temos alguns pontos a considerar. Primeiro, as janelas de tempo utilizadas aqui estão todas na faixa de dias, semanas e meses, enquanto que o fato estilizado
original preconizada uma comparação entre minutos e dias. Se a gente parar para pensar, a diferença de escala neste segundo caso é bem maior do que no primeiro caso, então só por aí já dá para desconfiar que o resultado pode sair diferente. Um segundo ponto é que estamos trabalhando aqui com volatilidade como sendo a variação entre dois quantis, quando normalmente ela é calculada como o produto do desvio-padrão pela raiz do tempo. Aí cabe um detalhe importante: originalmente este estudo foi feito utilizando este cálculo original, e o resultado não mudou quando troquei a fórmula.
Dias depois de eu ter fechado as duas imagens acima para começar a escrever este post, eu encontrei este artigo em que os autores tiraram a limpo todos os 11 fatos estilizados do artigo do Rama Cont, em que 8 deles foram devidamente
comprovados, 1 foi "não foi confirmado", e outro teve "suporte fraco". O fato estilizado que teve o "suporte fraco" foi justamente o que analisamos aqui, o que mostra
que "não estamos sozinhos nessa". E isso porque não só os dados utilizados pelos autores são completamente diferentes do que usei aqui (eles usaram dados de intra-day
e de diário de 10 ações, dados estes obtidos diretamente de corretoras dos Estados Unidos), bem como a metodologia usada para avaliar também foi completamente
diferente.
Apesar disso, ele trazem uma observação interessante: o paper de Rama Cont foi lançado em 2001. Desde então, a regulação americana de compra e venda de ativos em
bolsa mudou drasticamente (você avalie no Brasil). Por causa disso, é de certa forma natural que a dinâmica das negociações de ativos, e mesmo das flutuações,
também tenha mudado, afetado em algum ponto o comportamento estatístico destas flutuações. Além disso, é importante considerar que a dinâmica do mercado de renda
variável é fruto não só do seu contexto histórico mas também do comportamento e fator humano, que aliado às mudanças nas legislações, muda a forma de operação.
Epílogo
Foi muito curioso ver que uma simples análise não só levou a resultados em direções opostas às de um paper seminal, bem como ver que outro estudo conduzido de forma
completamente diferente chegou à uma observação muito próxima. Este tipo de resultado tem um impacto adicional ainda, pois, no artigo de Cont, estes fatos estilizados
também se configuram como propriedades das quais modelos que simulam a flutuação de preços de ativos deveriam ter. Como o tempo passou e a legislação mudou, vemos que
realmente é necessário dar uma "reciclada" nestas propriedades. Além disso, é importante considerar que o artigo é de 2001 (23 anos atrás em relação ao tempo da
escrita deste post). Em ciência, artigos com idade a partir de 5 anos já são considerados "antigos", sendo necessário estudar artigos mais recentes para checar
as novidades. Por conta disso, é natural que conclusões obtidas há um bom tempo sejam refutadas/corrigidas/etc.
Conforme mencionei no início do post, os códigos e dados da análise estão disponíveis neste link, e para quem curte analisar dados, fica como dever de casa não só explorar essa análise desta vez considerando dados de intra-day,
como também testar em outros ativos (ações individuais, outros ETFs etc.), bem como verificar se alguma volatilidade longa individual conseguiu ainda assim ter Informação Mútua melhor que alguma Volatilidade Curta. Outra coisa a se testar seria trocar a métrica de avaliação: ao invés de usar Informação Mútua, usar correlação, por exemplo.
Até a próxima postagem!
Aug 18, 2024
Surpresa! Dei um "unpause" no blog! Depois de aproxidamente um ano e meio,
consegui arrumar um tempo e montar um estudo especial sobre o portfólio de Ray Dalio,
personalidade do mercado financeiro que inspirou e inspira muitos,
os quais me inspiraram a criar esse blog. Sem mais delongas, fiquem
com o estudo!
Ray Dalio é uma figura bastante conhecida no mundo dos investimentos e mercado
financeiro por várias coisas. As principais delas são seu livro de princípios e o seu "All Weather Portfolio",
que trabalha com ideias ligadas à paridade de risco. As ideias por trás do portfolio são as seguintes:
- Ele é composto por "classes de ativos" que são descorrelacionadas entre si
(ou pelo menos próximas disso);
- A composição do portfolio permite que ele tenha bons resultados em qualquer
momento econômico (seja ele bonança ou crise).
- A composição do portfolio permite que ele tenha uma volatilidade reduzida em
relação às classes de ativos (ou mesmo nos ativos) de individualizadas, logo
o "risco de investimento" é "minimizado".
A ideia do post é aqui, então, é a gente "tirar isso a limpo" e ver se a coisa
realmente bate. Parafraseando Ian Neves,
"começando pelo final", a coisa realmente bate. Bate 100%? Não, mas chega muito
perto (só não bate 100% "por besteirinha"). Vamos lá?
Primeiros passos
O primeiro passo é saber quais classes de ativos utilizar e suas percentagens
no portfolio. Segundo este artigo, são elas:
- Ações dos EUA (30%)
- Tesouro Direto dos EUA de longo prazo (40%)
- Tesouro Direto dos EUA de prazo intermediário (15%)
- Commodities (7.5%)
- Ouro (7.5%)
Vou ficar devendo a referência de onde tirei os tickers que utilizei para
puxar os dados, mas, respectivamente, são eles: VTI, TLT, IEF, DBC e GLD.
O artigo do Seeking Alpha que citei também fornece os tickers, porém ele
foi acessado depois que fiz a análise, para a escrita deste blog (falha
minha). De toda forma, é importante destacar que há uma discrepância muito
grande entre sites quando se fala de quais tickers utilizar. Apesar de tudo
isso, os tickers que usei são exemplos comuns das classes de ativos utilizadas
para o portfólio, então vale o uso deles.
O próximo passo foi baixar os dados. Para isso, utilizei a biblioteca Python
yfinance, que baixa os dados OHLC (Open,
High, Low, Close) do Yahoo Finance. O código que
fiz para esta análise está todo em Python, disponível aqui.
Informação importante: os dados de cada classe de ativos, por causa da
disponibilidade do Yahoo Finance, tem diferentes "datas de inicio" (apesar de
terem a mesma "data de fim", que foi 8 de agosto de 2024). A gente vai ver
mais na frente que foi feita correlação par-a-par, e neste caso acabaram sendo
utililzados "diferentes intervalos" para cada par, buscando maximizar o tamanho
do intervalo. Dito isso, a data inicial mas antiga obtida dos dados é 15 de
junho de 2001 e a mais recente é 6 de junho de 2006. Somente uma classe (Ações
EUA) tem essa data mais antiga e também uma só (Commodities) tem a mais recente.
As duas classes de "Tesouro Direto" tem início em 2002 e Ouro tem início em
2004. Ou seja, as análises de correlação vão pegar períodos variando entre
18 e 22 anos.
Processando os dados para a análise
De posse dos dados, a próxima tarefa foi calcular as duas principais métricas
para fazer a análise: retornos das classes de ativos e correlação. Para cada
classe, foram calculados retornos diários através do logaritmo natural da
divisão do preço de fechamento de cada data sobre o preço de fechamento da
respectiva data anterior. De posse destes retornos, foram calculadas
correlações de Pearson
entre cada par de classes. Estes mesmos retornos também foram utilizados para
"tirar a limpo" as ideias ligadas ao desempenho do portfolio.
Agora sim vamos "tirar a limpo" as ideias do porfolio de Ray Dalio.
Tirando a limpo a correlação
A ideia das classes de ativos serem descorrelacionadas entre si é justamente
para que quando uma das classes estiver indo mal, alguma outra consiga
compensar o prejú. Na prática, só ter a classe não basta, tem que ajustar as
proporções também, isso é um pilar essencial, por isso citei no início do
post. Apesar da gente não explorar as proporções nesta análise, nós vamos
nos utilizar delas nas análises de desempenho, para calcular o desempenho do
portfólio.
Mas beleza, hora de tirar a limpo a questão da correlação:
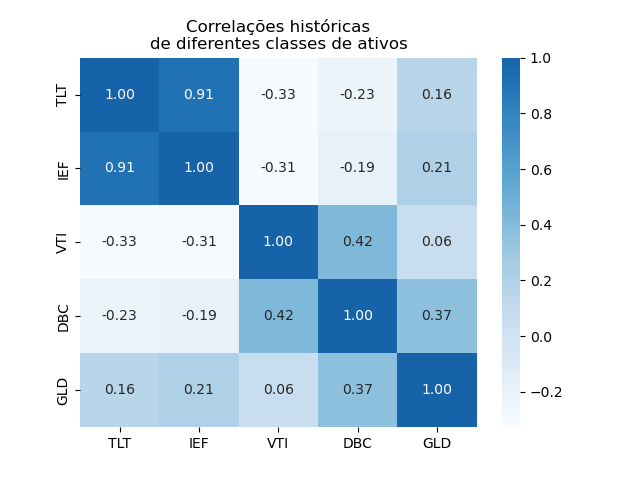
Figura 1 - Correlação entre as classes de ativos
Nota rápida: correlações positivas indicam que os retornos dos pares de
classes estão na mesma direção. Correlações negativas indicam direções opostas
(que idealmente é o que queremos, para gerar o equilíbrio da coisa).
Um rápido guia para interpretar os valores: até 0.3 a correlação é fraca, então a
coisa está descorrelacionada mesmo. Entre 0.4 e 0.6, a correlação é moderada,
ou seja, tem um "cheirinho" de correlação começando (esse site trás umas ilustrações
legais de conferir esses comportamentos). De 0.7 para frente já era, temos
correlação na parada.
Com base nisso, podemos dizer que no geral, esse lance de ser tudo
descorrelacionado base quase 100%. Isso porque as duas classes de "Tesouro
Direto" tem correlação próxima de 1, e os pares ações-commodities e
commodities-ouro tem correlações moderadas (ou seja, esboça-se um início de
correlação na parada). Isso denota que mesmo que você tente abarcar "toda a
diversidade do mercado" (que no fundo é o que Dalio tenta fazer), vão ter
momentos em que "aproxiadamente" esse lance de compensação vai é pro ralo,
e todo mundo "aproximadamente" ruma para uma direção só (seja alta ou baixa).
Isso implica que, de certa forma, se você quiser trabalhar com menos classes
ainda, é possivel.
Apesar da grande maioria de pessoas e "gurus" no mercado financeiro, incluindo
o próprio Dalio, incentivarem a diversificação de investimentos, defendendo
justamente a questão de minimização da volatilidade/risco, há alguns aqui e
ali que defendem justamente o oposto. Como diria Buda, "o melhor caminho é
o do meio". Pela matriz acima, é possível ver que daria para tirar, num
primeiro momento, uma classe ou outra para garantir o descorrelacionamento
entre todo mundo.
Além dessa matriz, eu também fiz o seguinte: calculei correlações par-a-par
de classes, desta vez utilizando janelas de 22 dias ("um mês"). A partir destas
janelas contei quantas vezes a correlação entre cada par ficou acima de 0.5 ou
acima de 0.7. Segue o resultado:
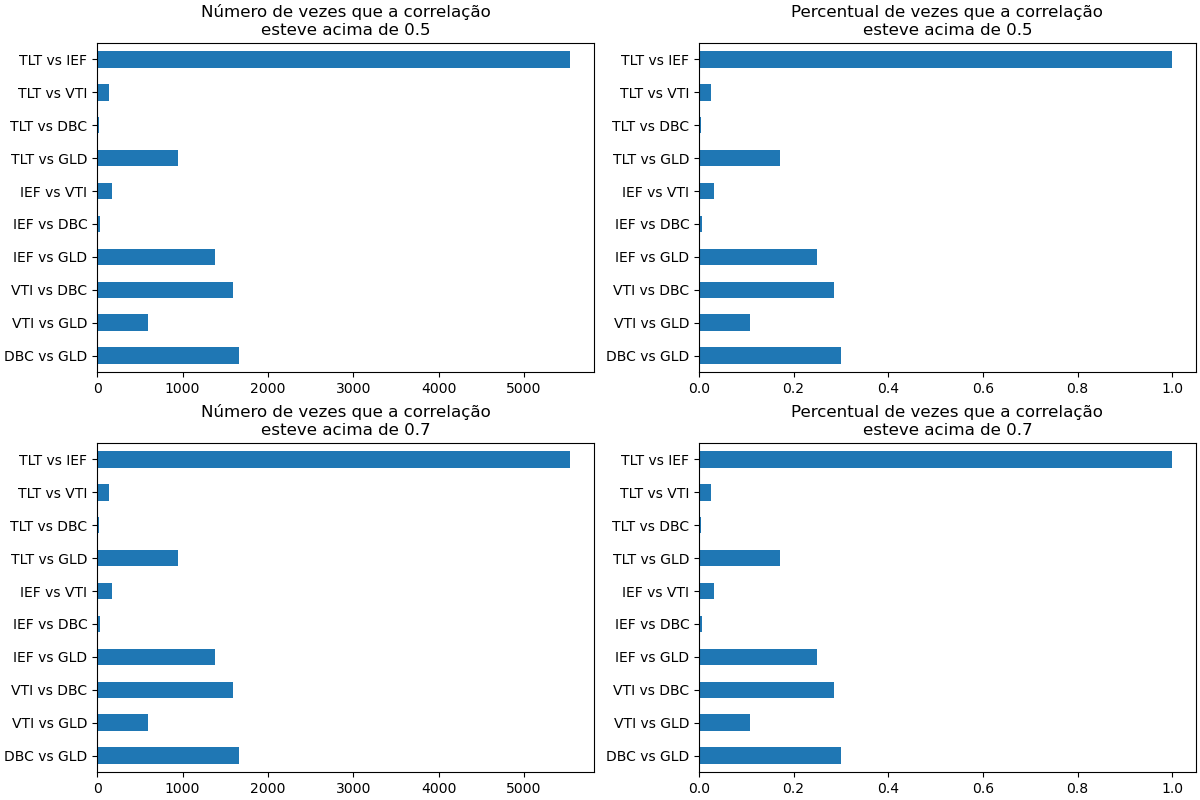
Figura 2 - Número de vezes em que os pares de classes tiveram correlação moderada ou forte
Como podemos observar acima, ao longo dos últimos 20 anos houve uma quantidade
não-desprezível de vezes em que as classes rumaram numa mesma direção. Apesar
disso, podemos destacar os pares "Tesouro Direto (Longo ou Intermediário)-Commodities",
com uma quantidade quase nula de vezes, e o par "Tesouro Direto Intermediário-Ações",
com uma quantidade bem pequena também. Isso reforça a ideia de que talvez não se
precise montar um portfolio com muita coisa diferente, principalmente se
você for pessoa física com não muita grana (mas não tomem isso como recomendação).
Agora vamos tirar a limpo questões ligadas ao desempenho do portfolio.
Desempenho do portfolio
Para calcular o desempenho do portfolio como um todo, primeiro eu "alinhei"
os retornos de cada classe pela data. Este alinhamento faz com que os dados
se iniciem em 2006, pelos motivos comentados anteriormente na parte das
correlações. Para o conjunto de retornos por data, multipliquei cada retorno
pela sua respectiva percentagem e depois somei tudo. Dessa forma, temos os
retornos do portfólio por data, e assim podemos fazer comparações com as
outras classes.
A primeira coisa que vamos "tirar a limpo" é se o portfolio realmente tem
bom desempenho em qualquer momento do mercado. Para isso, vamos avaliar se
ele pelo menos fica no positivo (entre muitas aspas) sempre. Para avaliar
isto, apliquei janelas deslizantes de 20 ("1 mês"), 60 ("3 meses"), 252 ("1 ano"),
756 ("3 anos"), 1260 ("5 anos"), 2520 ("10 anos") e 3780 ("15 anos") dias,
usando a função soma como agregação. Com isso temos o retorno do portfólio
em "todos os possíveis períodos contínuos de cada janela". A tabela 1 ilustra
as percentagens de períodos em que o portfólio teve resultado positivo, alguma
das classses teve resultado positivo (no mesmo período) e se o portfólio foi
negativo e alguma classe foi positiva em um mesmo período.
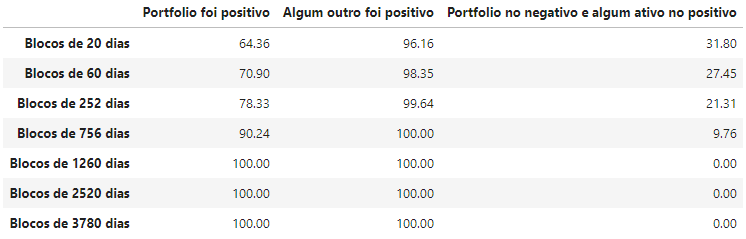
Tabela 1 - Percentagens de resultados positivos para o portfólio comparado com outras classes
Aqui temos um comportamento curioso: quando a gente "aumenta o zoom" colocando
a janela para um período bem pequeno, vemos que o portfólio sofre consideravelmente,
mas à medida que vamos "diminuindo o zoom" o efeito do retorno vai sendo visível, ao
ponto que na janela de 1260 dias (5 anos) o porfólio sempre apresenta resultado
positivo, independente da início desde 2006. O mesmo vale para classes "de
forma geral" (numa janela de 10 anos sempre alguma delas vai estar no positivo).
Isso mostra que portfólio é um investimento para se segurar e trabalhar no médio
e longo prazo, não no curto (o que, de certa forma, "é o esperado").
Outra tabela que montei é a percentagem de vezes em que cada classe tem o maior
retorno em cada tipo de janela de tempo diferente (Tabela 2).
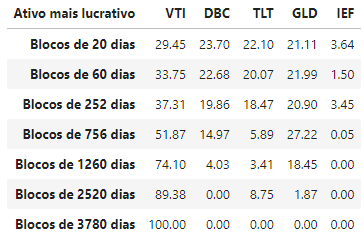
Tabela 2 - Percentagens de vezes em que cada classe tem o maior retorno em cada janela de tempo
Aqui podemos observar algumas coisas interessantes: independente da janela de tempo,
a classe "Ações EUA" sempre tem a maior percentagem melhor desempenho, chegando a
ser a única com melhor desempenho na janela de 15 anos. Além disso, a classe
"Tesouro Direto EUA de Longo Prazo" sempre abocanha alguma fatia até a janela de
10 anos, e o Ouro também. "Tesouro Direto EUA de Prazo Intermediario" sempre tem
uma fatia bem pequena até a janela de 3 anos (curiosamente, os prazos dos títulos
intermediários presentes no IEF variam de 3 a 10 anos, então isso explica um pouco).
E finalmente, olhando para a tabela, é como se houvesse um "comportamento
de cauda longa nela". Além
disso, percebam que Commodities, Títulos Longos e Ouro tem percentagens próximas
entre si nas janelas até 1 ano.
Para fazer a reflexão sobre isso, trago de volta as percentagens de alocação
do portfólio:
- Ações dos EUA (30%)
- Tesouro Direto dos EUA de longo prazo (40%)
- Tesouro Direto dos EUA de prazo intermediário (15%)
- Commodities (7.5%)
- Ouro (7.5%)
Não por acaso ações e títulos longos tem o maior percentual: ações é o carro
chefe do rendimento, seguido dos títulos longos (pelo menos pelo que vemos
na tabela). Esse balanço Ações vs Títulos é um modelo interessante ao ponto
de existirem modelos de portfólio que envolvem somente estas duas classes.
E de fato, a gente observa que a correlação entre eles é negativa (-0.33), e
que são "raros" os momentos que eles apresentam alta correlação (vide Figura 2).
Dessa forma, é natural 70% do portfólio ser composto por eles. Eu suponho que
adicionar as outras classes acabe sendo muito mais com um objetivo de fazer
proteção e diminuir ainda mais volatilidade do que necessariamente aumentar
os retornos.
Para fechar este post, trago um painel simples de métricas e curvas de retorno
do portfólio e de cada classe individualmente (considerando todo o período
desde 2006):
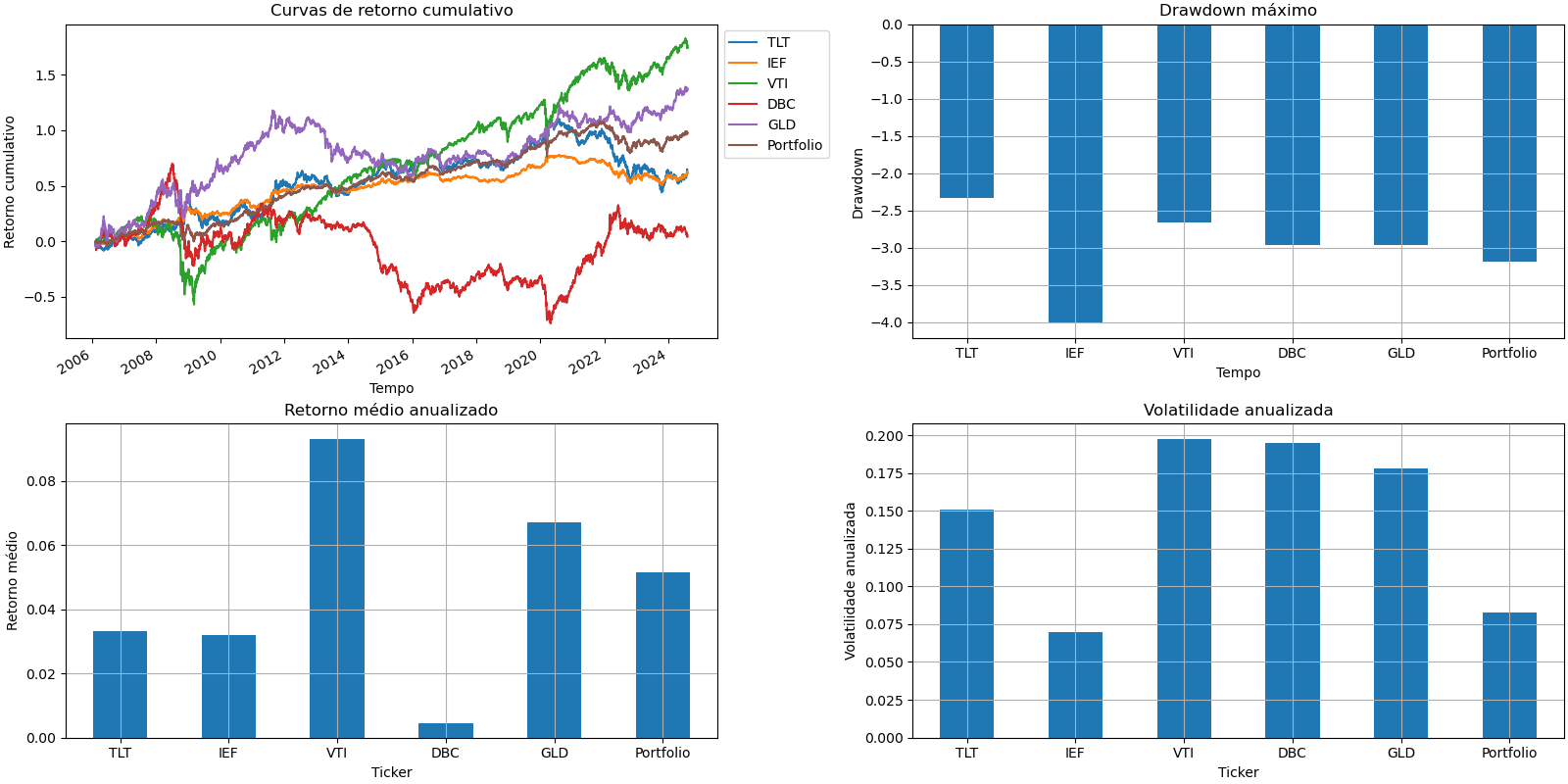
Figura 3 - Painel de métricas de desempenho de portfólio e classes individualizadas
Conforme esperado, o portfólio apresenta uma volatilidade menor que a de todas
as demais classes com exceção dos títulos de prazo intermediário. O retorno
médio por ano encontra-se maior que os títulos e menor que ouro e ações, o que
também é algo esperado dada sua composição. Considerando que as taxas de juros
americanas estão na faixa dos 5.5%
em agosto de 2024, dá para se ver que o portfólio na média "deixa a pessoa no 0
a 0", isso se não tiver um "pequeno lucro". Olhando para as curvas, nota-se que
o portfólio só perde justamente para ações e para o ouro. O que se pode estranhar
a princípio é que, apesar de tudo isso, o drawdown máximo do portfólio foi maior
que o de todas as classes com exceção dos títulos de médio prazo. Uma explicação
que poderiamos dar para isso seria justamente a combinação dos ativos, ao dar
poder de retorno, também contribui para o prejuízo. Queiramos ou não são 40%
alocados em ações, então acaba sendo uma contribuição considerável.
Para fechar o post
O portfólio do Ray Dalio realmente "cumpre" com a sua ideia de diminuir o risco
em comparação às classes de ativos individualizadas e oferece um retorno médio
interessante se comparado com a "renda fixa". Mesmo apresentando momentos de
prejuízo no curto prazo, o portfólio no longo demonstra ser realmente rentável.
Além disso, a análise de correlação mostrou que se quiser, dá para "enxugar" ele
ainda mais. E pensando num cenário de pessoa física montando seu próprio portfólio,
a máxima "menos é mais" é essencial.
Apesar de não ter sido explorado aqui, os percentuais de alocação dados para
classe de ativos são um aspecto tão importante quanto as próprias classes, uma
vez que são eles quem trazem a diminuição da volatilidade. Por causa disso, mesmo
que se resolva tirar uma classe ou duas (exemplo, Títulos de prazo intermediário e
commodities), é necessário estipular novos percentuais para que a propriedade de
volatilidade reduzida permaneça.
No fim das contas, é um portfólio mais voltado para quem coloca "segurança" como
prioridade na hora de investir, mas não quer deixar de aproveitar bons retornos
trazidos por classes mais "agressivas". Um aspecto interessante deste portfólio
é que ele não utiliza a classe dos REITs ("fundos imobiliários") na sua composição,
e não "isola", por exemplo, o petróleo, tal qual fez com o ouro. Tais "substituições"
(ou "adições") são pontos interessantes para se analisar.
Para fechar, fica o lembrete: não tem essa análise como recomendação de compra
ou venda. É como dizem, "retornos passados não garantem lucros futuros". Além
disso, investir em renda variável involvem pagar uma série e taxas e impostos
que não foram cobertos nesta análise, e que na prática afetam e muito a
rentabilidade do portfólio. Façam seus próprios estudos também e procurem
especialistas do teu banco ou da tua corretora para ajuda antes de tomarem
qualquer decisão.
Parafraseando o que falo na página de página de metodologia,
caso vocês notem algum erro, ou tenham alguma dúvida sobre alguma coisa neste post e nos outros,
não deixem de entrar em contato comigo pelo e-mail contemplandoomercado@gmail.com.
A propósito, caso queiram ver por aqui algum novo estudo, é só falarem também.
Epílogo
Espero que tenham curtido esse "unpause" no blog. Infelizmente não posso prometer voltar
com as análises mensais de antes, uma vez que minha capacidade de fazer os posts de forma
recorrente (por hora) foi para o espaço. Por causa disso, o blog vai acabar funcionando
no "modo golfinho" (aparece, faz uma gracinha e some) trazendo algum estudo especial.
Até a próxima postagem!
Jul 28, 2022
Galera, as análises do mês de Julho de 2022 vão demorar um pouco mais sairem,
muito provavelmente em torno da segunda quinzena de agosto. Por causa disso,
deixo para vocês uma "análise de sazonalidade" das classes de ativos a partir
de 2000.
No post anterior, eu havia comentado que
em um estudo que fiz ano passado, eu verifiquei que o mês de Julho, para
praticamente todo tipo de ativo em renda variável, é caracterizado,
na média, por ser de alta. Pois bem, inspirado nisso, eu resolvi refazer
esse estudo e trazer para o blog. Uma coisa legal dele é que ele está
abrangendo Julho de 2022 também, então já vai dar para termos uma noção
do que está rolando neste mês.
Basicamente vamos trabalhar na seguinte pergunta: "se desde 2000 (ou um pouco
depois, a depender do início da série histórica que estamos usando) a gente
todo ano tivesse comprado um ativo sempre no início de um mês específico e
depois tivesse vendido no final o 'mês específico', qual teria sido o retorno?"
Nesta análise, nós vamos trabalhar com quase todas classes que já estamos
acompanhando por aqui. Dessa vez, Urânio (URA) e REITS (VNQ) ficaram de fora,
e ações da NASDAQ (QQQ) entraram no lugar.
Outra coisa importante: desta vez não trabalharemos com prêmio de risco, e sim
com os "retornos brutos" (sem descontar nada).
Retornos médios
Vamo lá. Vamo dar uma olhada em quanto cada classe deu de retorno em média
em cada mês.
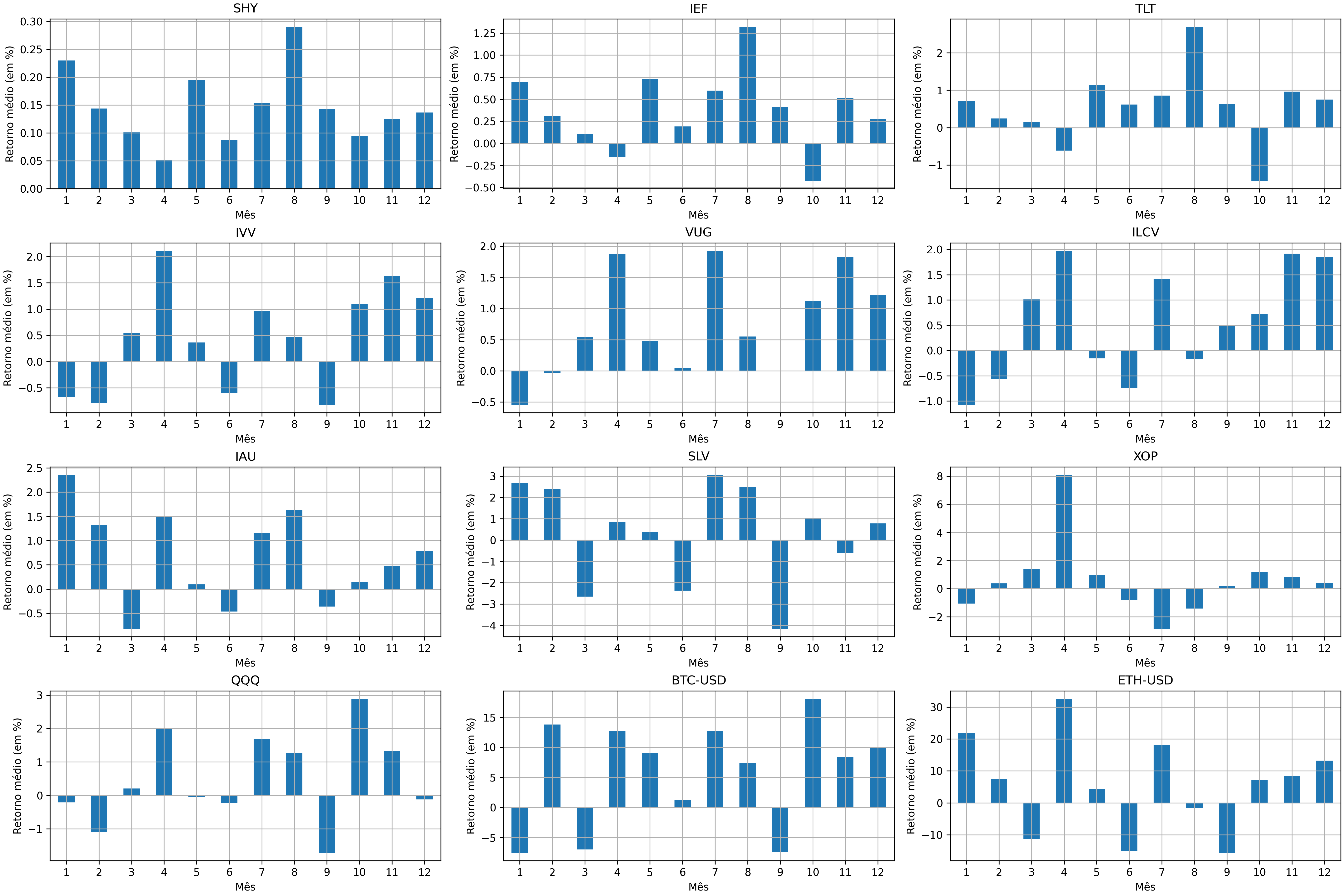
Figura 1 - Média dos retornos das classes de ativos em cada mês
Logo de cara já temos aquela surpresa: Títulos Públicos de curto prazo (SHY)
tendo média positiva em todos os meses (?!) Pode isso, Arnaldo? E é
nessas horas que aparece a "pegadinha": esses números são médias, ou seja,
certamente em um ano ou outro rolaram retornos negativos. De toda forma, é
importante lembrar que estamos falando de um dos investimentos mais seguros
do mundo, que é a renda fixa do Estados Unidos, logo é de se esperar bons
resultados. E percebam que os retornos são baixinhos: o maior deles foi de
0.30%, em agosto. É aquela velha máxima do risco-retorno: menos risco, menos
retorno (e vice-versa). Outro ponto importante: esses títulos possuem entre 1
e 3 anos de vencimento, então em teoria a volatilidade deles deve ser baixa.
Analisando Títulos Públicos dos EUA de curto prazo
Voltando para a questão central do estudo, mais especificamente em SHY: se
tivéssemos feito "trades mensais" em SHY, como teria sido a curva de retorno
para cada mês? A figura abaixo nos traz a resposta:
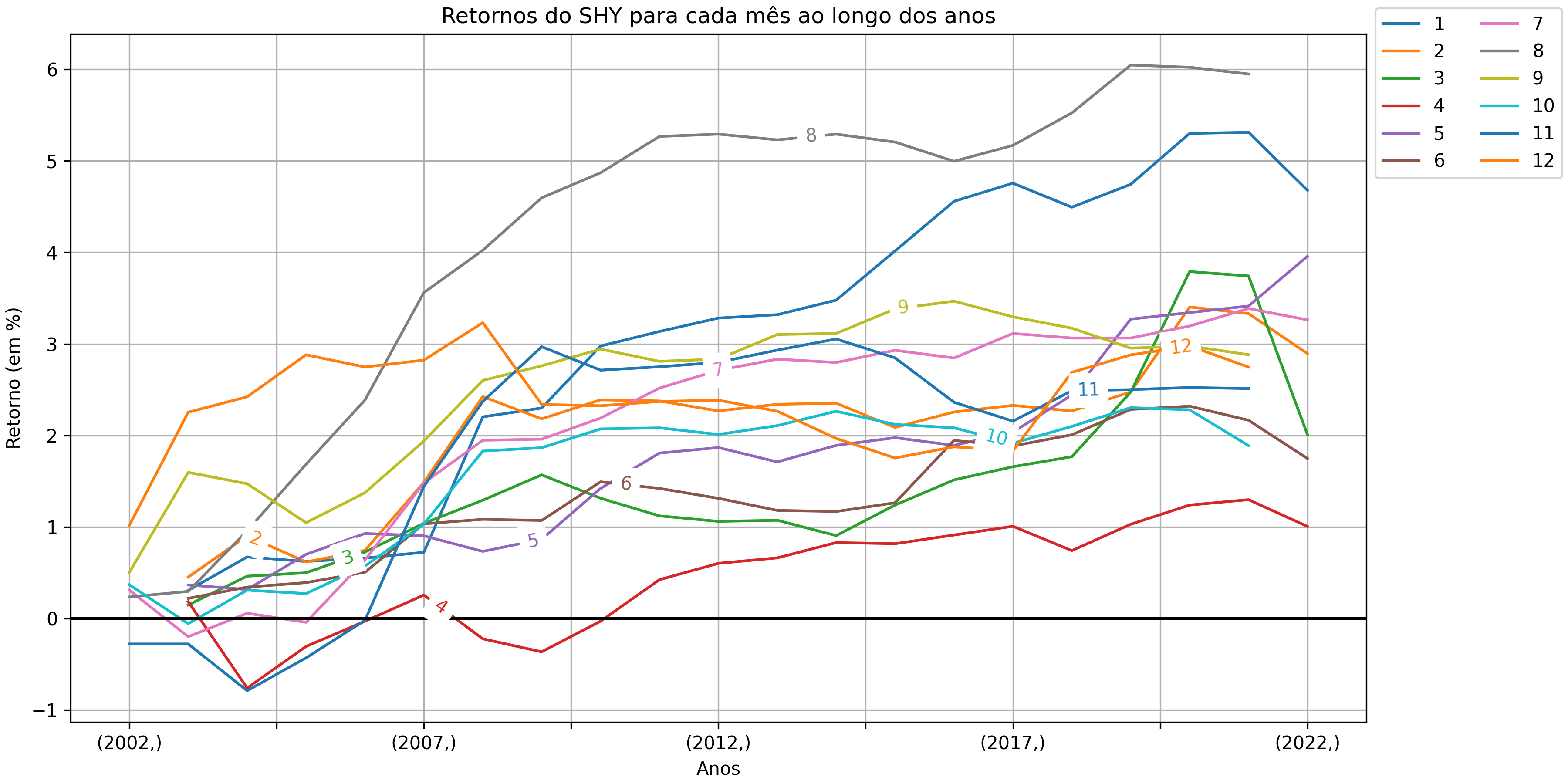
Figura 2 - Curva de retornos mensais dos Títulos Públicos de curto prazo dos EUA
Como podemos perceber, a figura mostra claramente que os Títulos Públicos de
curto prazo passaram de fato por períodos de queda, apesar de registrarem
média positiva todos os meses. O primeiro destaque nisso vai para o mês de
Abril (mês 4), que literalmente "ficou no vermelho" entre 2002 e 2004, e entre 2008
e 2010 (curiosamente, a época do subprime.
É... nem mesmo a renda fixa se salvou nessa época). Percebam também que os
retornos de alguns meses tem caído nos últimos anos, com destaque para
Janeiro (mês 1), Março (mês 3), Junho (mês 6), e o próprio Abril. Por outro
lado, percebam que a curva de retornos considerando o período histórico com o
qual estamos trabalhando é positiva, "corroborando" assim as médias positivas,
com destaque para o mês de Maio (mês 5), que fecha a curva em 2022 subindo.
Meses de Lucros e Crises
Voltando nossos olhares para a Figura 1, vamos agora nos concentrar nas barras
correspondentes ao mês de Julho (mês 7). Se a gente parar verificar,
perceberemos que, com exceção de petróleo (XOP), todas as classes possuem
retornos positivos no famoso "mês das férias", com destaque para as criptos
(BTC-USD e ETH-USD), com médias próximas dos 20%. Percebam também outra coisa:
as médias de Julho (bem como de outros meses) concentram-se entre 1% e 3%.
Multiplicando isso por 12 (para termos uma noção de retorno anual), isso fica
entre 10% e 30%. Isso condiz com algo que é bastante comentado de que o
rendimento médio de "bons investidores" no longo prazo fica em torno de
20% ao ano.
Vamos agora facilitar um pouco nossa vida de visualizações com a figura
a seguir:
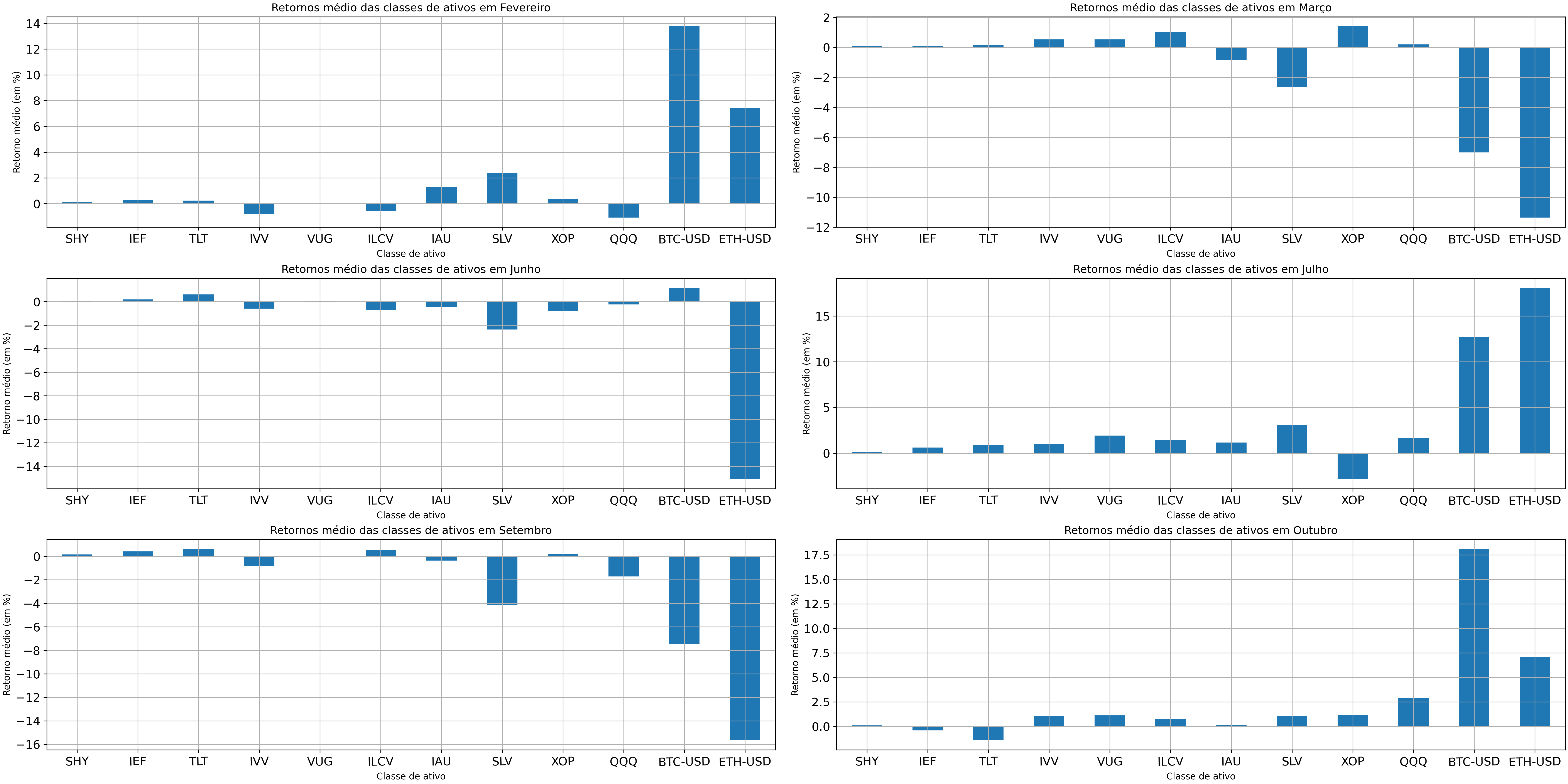
Figura 3 - Médias dos retornos das classes dos ativos em diferentes meses
As escolhas dos meses acima (com exceção de Junho e Julho) não foi por acaso:
alguns dos crashs mais famosos da história aconteceram neles: Crise de 1929,
Black-Monday de 1987, Bolha das Ponto-Com de 2000, Crise do Subprime em 2008,
Crash das Criptos de 2018, Flash-Crash da COVID-19... todas ocorreram em algum
destes meses, a maioria entre Setembro e Outubro. E a figura acima corrobora
isso: percebam que a média o S&P 500 (IVV) está caindo em Fevereiro, Junho e
Setembro, voltando sempre a se recuperar no mês seguinte. Um ponto curioso:
a renda fixa dos EUA (SHY, IEF e TLT), com exceção do mês de Outubro, fica
positiva nestes meses, daí muitas carteiras de investimento colocarem parte
de suas posições nelas, para dar um pouco de equilíbrio e diminuir um pouco
o risco.
Outra ponto: "como sempre", em todos estes meses as criptos apresentam
comportamentos bem exagerados (para cima ou para baixo). Agora um fato curioso:
Michael Burry
tuitou em Junho de 2022
uma imagem da Bloomberg mostrando o quão parecido era o movimento do Bitcoin
com o da NASDAQ, e ainda provocou: Temos certeza de que Bitcoin não é só
mais um ativo de risco da NASDAQ? Além disso, eu mesmo já vi comentários
de Bitcoin seria nada mais do que "uma aposta alavancada no mercado de ações",
pelos mesmos motivos de movimentos equivalentes. Pois bem, a figura acima nos
evidencia uma coisa curiosa: no segundo semestre isto de fato acontece (e
realmente o BTC aparenta ser um ativo de risco da NASDAQ e uma aposta alavancada
no S&P), porém no primeiro semestre a movimentação é o exato oposto: enquanto
um sobe, o outro cai. Analisando a matriz de correlação histórica que postamos
no início deste mês, veremos que a correlação
Ações-Criptos é de 0.45, sendo (0.17 no período Abr-Jun/2022). Pegando
emprestado o modo de falar do Rytenband,
dá pra explorar algumas boas assimetrias entre Ações e Criptos ao longo do ano
(principalmente no primeiro semestre).
"Trading mensal" em Julho
Para fechar as análises, vamos dar uma olhada em como sairiam as curvas de
retornos das classes de ativos se comprássemos no início de Julho e
vendêsssemos no final dele.
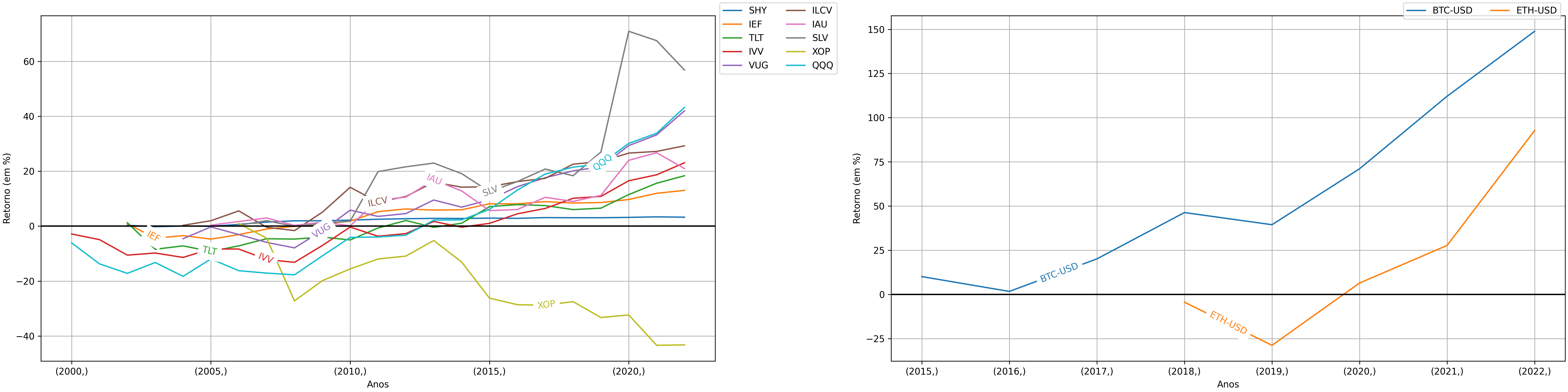
Figura 4 - Curva de retornos das classes de ativos em Julho
Corroborando mais uma vez com o que já vimos antes, Julho de fato demonstra
ser um mês em que classes de ativos sobem. No entanto, é importante perceber
que isso só começa a ocorrer de fato "para a grande massa" a partir de 2010:
notem que antes disso as classes andaram de lado e tiveram até mesmo retornos
negativos. Outro fator interessante: notem que a classe que mais rendeu não
foi nem o S&P 500 (IVV), nem o NASDAQ (QQQ), e nem mesmo Growth Stocks
(VUG)! Quem rendeu mais foram as Value Stocks (ILCV), com um pouco menos de
60%. Isso é interessante, pois evidencia aquela máxima de que "os fundamentos
são o que importa no fim das contas". Muita gente forte do mercado, como o
próprio Rytenband, defende bastante essa ideia.
E mais uma vez as Criptos apresentam retornos absurdamente altos, tanto
que tive que montar um gráfico separado para melhorar a visualização.
Percebam que entre 2018 e 2019 o retorno das criptos caiu, mesmo se
tratando do mês de Julho (para a gente ver como o crash foi forte). Em
compensação, bastou passar um único ano para "as máximas se renovarem".
Finalizando o post
Bem galera, o post de hoje mostrou que de fato Julho é um mês bastante
lucrativo para a grande maioria das classes de ativos, e que realmente os
fundamentos levam a melho no jogo do longo prazo. Vimos também que os Títulos
Públicos de Curto Prazo são uma classe bastante interessante a se considerar
e estudar quando se pretende montar uma carteira de investimentos de longo
prazo, e que Criptos, para a direção que for, são verdadeiros "foguetes".
Um ponto que eu acabei não analisando neste post (e que deixo como dever
de casa) é o mês de abril. Reparem no retorno médio do Petróleo (XOP) neste
mês, e comparem com outros meses. Tem algo de interessante aí.
Particularmente achei bem legal fazer esse estudo. Espero que ele possa
ajudar vocês de alguma forma caso pensem em algum momento em montar uma
carteira de longo prazo, ou até mesmo fazer aquela especulação marota
(só lembrando para não tomarem nada deste post como recomendação de compra
e venda). Parafraseando o que falo na página de metodologia,
caso vocês notem algum erro, ou tenham alguma dúvida sobre alguma coisa
neste post e nos outros, não deixem de entrar em contato comigo pelo e-mail
contemplandoomercado@gmail.com. A propósito, caso queiram ver por aqui
algum novo estudo, é só falarem também.
Até a próxima postagem!










