Análise Especial - O Fato Estilizado número 11 de Rama Cont
Deparei-me recentemente com este post do Kadima Asset Management no Instagram que falava sobre Fatos Estilizados. Este termo curioso é referente a um artigo do pesquisador Rama Cont que fala sobre propriedades estatísticas comuns a diversos ativos (e classes) do mercado financeiro. O artigo lista 11 fatos estilizados, dos quais o último (dentre outros) me chamou à atenção, e aqui trago a tradução trazida pelo post do Kadima Asset Management:
Assimetria nas escalas de tempo: Medidas de volatilidade em escalas de tempo mais amplas preveem a volatilidade em escalas de tempo mais curtas do que o contrário.
Este fato estilizado me chamou à atenção por ser um fato que podemos analisar de maneira relativamente simples (e, claro, empírica). Por causa disso, resolvi "tirar isso a limpo" e fazer uma análise de se isso acontece ou não.
Primeiro passo: selecionando os ativos e coletando os dados
Resolvi testar o fato estilizado em ativos relacinados a índices de bolsas de valores, tesouro americano, commodities, ouro e Bitcoin. A lista abrangendo os tickers de cada ativo e uma breve descrição deles pode ser conferida abaixo, montada pelo Perplexity (prompt aqui).
Aqui está a tabela em markdown, escrita em língua portuguesa, com os tickers solicitados:
| Ticker | Descrição |
|---|---|
| ^GSPC | Índice S&P 500, que representa as 500 maiores empresas de capital aberto dos EUA. É considerado um dos principais indicadores do mercado de ações americano. |
| ^BVSP | Índice Bovespa, principal indicador de desempenho das ações negociadas na B3, a bolsa de valores brasileira. Reflete o comportamento das principais ações do mercado. |
| ^N225 | Índice Nikkei 225, o principal índice da Bolsa de Valores de Tóquio. Representa as 225 maiores empresas japonesas listadas na primeira seção da bolsa. |
| ^FTSE | FTSE 100, índice das 100 empresas com maior capitalização listadas na Bolsa de Londres. É um importante indicador do mercado de ações do Reino Unido. |
| ^GDAXI | DAX 40, índice das 40 maiores empresas da Bolsa de Frankfurt. Representa o desempenho das principais companhias da economia alemã. |
| VWO | ETF que busca acompanhar o desempenho de um índice que mede o retorno de ações de empresas localizadas em países de mercados emergentes. |
| AGG | ETF que busca acompanhar o desempenho de um índice que mede o mercado total de títulos de renda fixa com grau de investimento e tributáveis nos EUA. |
| GLD | ETF que busca refletir o desempenho do preço do ouro. Oferece aos investidores uma forma de investir em ouro sem a necessidade de armazenamento físico. |
| BTC-USD | Par de negociação Bitcoin/Dólar americano. Bitcoin é a primeira e mais conhecida criptomoeda descentralizada do mundo. |
| TLT | ETF que busca acompanhar o desempenho de um índice de títulos do Tesouro dos EUA com vencimento de 20 anos ou mais. |
| IEF | ETF que busca acompanhar o desempenho de um índice de títulos do Tesouro dos EUA com vencimento entre 7 e 10 anos. |
| VTI | ETF que busca acompanhar o desempenho de um índice que mede o retorno de investimento de todo o mercado de ações dos EUA. |
| DBC | ETF que busca acompanhar o desempenho de um índice composto por contratos futuros de 14 commodities amplamente negociadas. |
Assim como na análise do portfolio de Ray Dalio, utilizei aqui a biblioteca Python yfinance para baixar os dados OHLC (Open, High, Low, Close) do Yahoo Finance referentes a cada ticker (a propósito, os códigos da análise estão disponíveis aqui). Feito isso, vamos ao nosso segundo passo:
Calculando e avaliando a volatilidade
Tradicionalmente, a volatidade é calculada como sendo o produto entre o desvio-padrão dos retornos de um ativos em um determinado período e a raiz quadrada do período utilizado (para saber mais, veja este artigo da Investopedia e este artigo do Seeking Alpha). E eu digo a você: eu utilizei esta fórmula para calcular a volatilidade e fazer a análise. No entanto, ler o artigo de Rama Cont me fez "virar a chave" (finalmente) para um detalhe que eu em parte já entendia mas que nunca me tinha caído a ficha até então. A grosso modo, dados de mercado financeiro não seguem a distribuição normal (Gaussiana). Até aí tudo bem, quem mexe com finanças quantitativas já está careca de saber isso (inclusive o artigo traz boas discussões sobre isso e inclusive o autor dedica boa parte do trabalho às "caudas longas"). E aí vem o pulo do gato: a forma como o desvio-padrão tradicionamente calculado (confira esta lição da Penn State University para saber mais) leva consideração que os dados justamente seguem a distribuição normal! E agora?
Eu tive então a seguinte ideia: ao invés de calcular a raiz-quadrada da variância (forma tradicional), e depois multiplicar pela raiz do período, eu calculei a volatilidade como sendo a variação entre os "quantis" (ver este post para saber mais) de 95% e 5%, respectivamente, dos retornos no período. O cálculo de variação que usei foi basicamente o logartimo natural da divisão entre o quantil de 95% e o de 5%.
A ideia por trás disso é: períodos com alta volatilidade irão apresentar intervalos de valores maiores para a divisão definida acima, enquanto que períodos de volatilidade pequena irão assumir intervalor menores. O uso do logaritmo natural da divisão de valores inclusive é uma fórmula tradicionalmente utilizada em finanças quantitativas para calcular retornos, uma vez que produz resultados simétricos (ex: o "log_natural(2/3)", tirando o sinal negativo, vai produzir o mesmo resultado que "log_natural(3/2)").
Para poder avaliar e comaparar o poder preditivo de volatilidades longas e curtas, eu decidi me utilizar de uma métrica muito comum em Aprendizado de Máquina chamada Informação Mútua, que justamente traz uma forma de quantificar o poder preditivo de uma característica sobre outra. Apesar dela ser mais comumente utilizada em problemas nos quais você quer prever uma categoria, aqui a gente quer prever um número (para saber mais sobre, veja este link). Ainda assim, a biblioteca que usei para calcular ela tem um módulo adaptado para utilizá-la em problemas de "prever um número" (inclusive tem artigo que explica a diferença de uso). Observação final importante: quanto maior for o valor da informação mútua, maior será o poder preditivo da volatilidade. Ou seja: nossa hipótese aqui é que volatilidades longas terão informação mútua maior do que volatilidades curtas.
Agora que sabemos como fiz para calcular a volatilidade, vamos ao nosso terceiro passo:
Fazendo os experimentos
Para testar se uma volatilidade longa consegue prever uma volatilidade curta melhor do que o inverso, a gente precisa elicitar três coisas: quais períodos para volatilidades curtas utilizar, quais períodos para volatilidades longas utilizar, e para quais períodos futuros (quantos dias frente) testar. E aqui entra o ponto talvez mais crucial e delicado da análise: no artigo de Rama Cont, ele chama de volatilidade curta aquela com período de 30 minutos, e de longa aquela com período de 1 dia. Quando eu faço análises, eu utilizo normalmente dados diários (que foi o caso aqui),e infelizmente só vim me atentar que há uma forma de baixar dados de intra-day usando o yfinance no momento da escrita deste post, então deixo como dever de casa analisar intra-day versus diário. As volatilidades curtas e longas, assim como os períodos futuros para testar foram os seguintes:
- Volatilidade curtas: 2 dias, 3 dias, 5 dias e 10 dias
- Volatilidade longas: 1 mês, 3 meses, 6 meses e 1 ano (aqui eu considero "1 mês" como sendo 21 dias, e os demais períodos como sendo múltiplos de 21 dias. "1 ano" corresponderia a 252 dias (21 dias * 12 meses))
- Períodos futuros: 1 dia, 3 dias, 5 dias, 10 dias, 1 mês, 3 meses e 6 meses (na parte do mês, mesmo esquema de antes)
A ideia então foi calcular a informação mútua de todas as combinações possíveis dos valores acima e comparar os pares de volatilidades (por exemplo, a informação mútua de uma volatilidade de 1 mês sobre a volatilidade de 2 dias do dia seguinte, e vice-versa; a informação mútua da volatilidade de 1 mês sobre a volatilidade de 3 dias do dia seguinte, e vice-versa; e etc.). Detalhe importante, vamos ver isso para cada ativo da tabela da seção do Primeiro Passo.
Resultado do experimento (e discussão sobre)
Uma vez que a quantidade de combinações entre volatilidades e períodos futuros é bem alta, resolvi sumarizar os resultados em duas imagens. A primeira, a seguir, ilustra, para cada ticker de ativo da tabela do início deste post, as distribuições de Informação Mútua tanto para as Volatilidades Longas predizendo as Curtas (boxplots azuis) como para o inverso (boxplots laranjas), isso agregando todos os resultados para todos os períodos futuros.
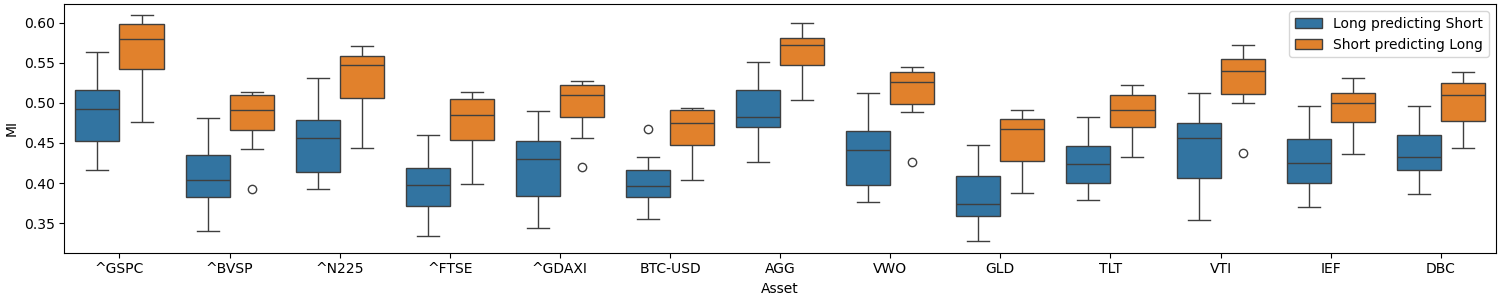
Figura 1 - Distribuição das Informações Mútuas obtidas para Volatilidades Longas predizendo Volatilidades Curtas e vice-versa
Conforme podemos observar, o resultado obtido é o "exato oposto" do que o fato estilizado diz: as volatilidades curtas possuem um poder preditivo melhor do que as longas! E pior: em ativos como o AGG e o VTI, a melhor Informação Mútua obtida para uma volatilidade longa bate no quartil de 25% da volatidade curta.
Aí a gente pode se perguntar: será que, para algum período específico, poderíamos ver volatilidades longas se saindo melhor que as curtas? Nisso, temos a segunda imagem, desta vez mostrando a média das Informações Mútuas dentre os períodos futuros para cada ativo:
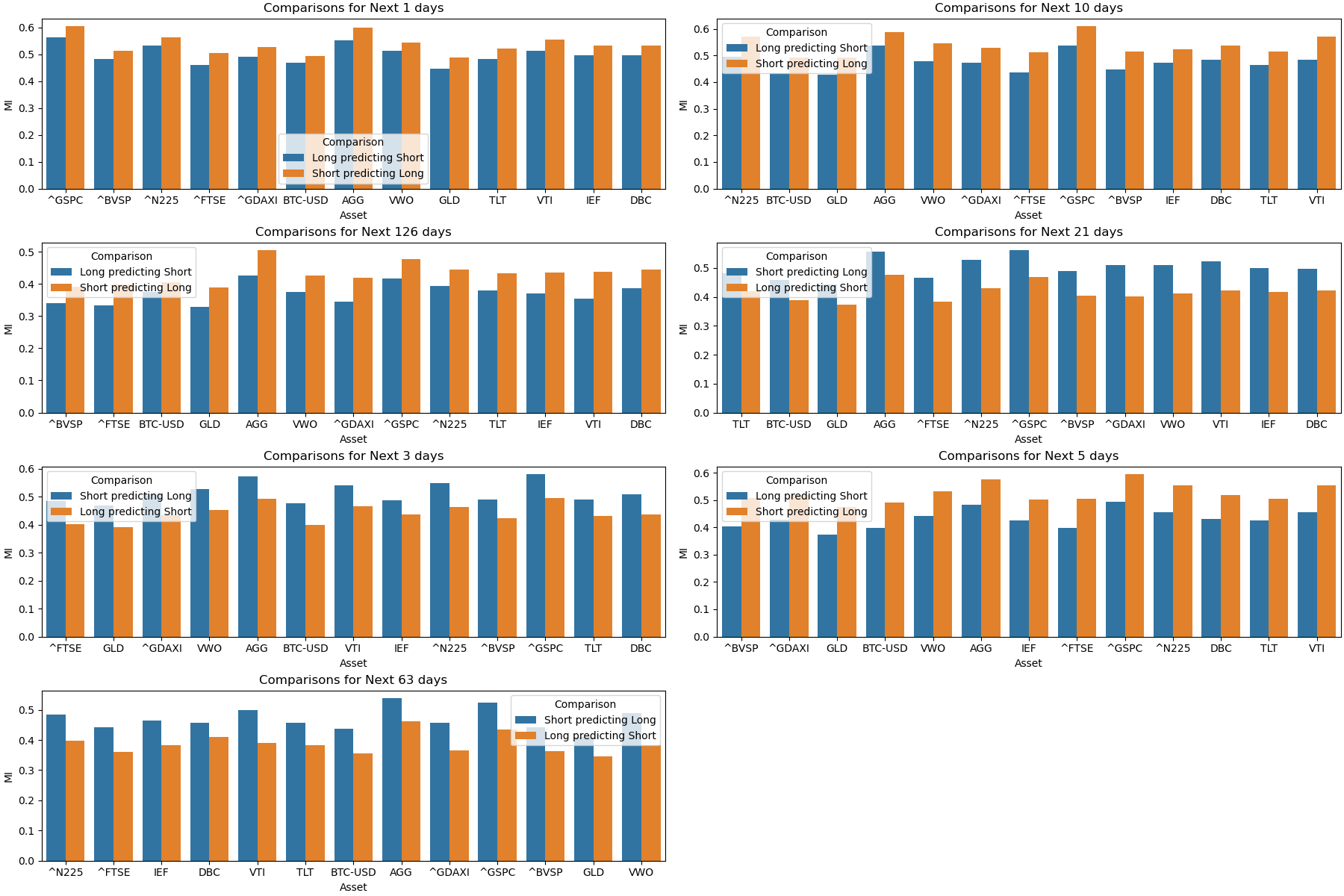
Figura 2 - Média das Informações Mútuas obtidas para Volatilidades Longas predizendo Volatilidades Curtas e vice-versa
E a resposta é clara: não. Em qualquer período futuro, a volatilidade curta tem poder preditivo melhor que a longa.
Nisso, temos alguns pontos a considerar. Primeiro, as janelas de tempo utilizadas aqui estão todas na faixa de dias, semanas e meses, enquanto que o fato estilizado original preconizada uma comparação entre minutos e dias. Se a gente parar para pensar, a diferença de escala neste segundo caso é bem maior do que no primeiro caso, então só por aí já dá para desconfiar que o resultado pode sair diferente. Um segundo ponto é que estamos trabalhando aqui com volatilidade como sendo a variação entre dois quantis, quando normalmente ela é calculada como o produto do desvio-padrão pela raiz do tempo. Aí cabe um detalhe importante: originalmente este estudo foi feito utilizando este cálculo original, e o resultado não mudou quando troquei a fórmula.
Dias depois de eu ter fechado as duas imagens acima para começar a escrever este post, eu encontrei este artigo em que os autores tiraram a limpo todos os 11 fatos estilizados do artigo do Rama Cont, em que 8 deles foram devidamente comprovados, 1 foi "não foi confirmado", e outro teve "suporte fraco". O fato estilizado que teve o "suporte fraco" foi justamente o que analisamos aqui, o que mostra que "não estamos sozinhos nessa". E isso porque não só os dados utilizados pelos autores são completamente diferentes do que usei aqui (eles usaram dados de intra-day e de diário de 10 ações, dados estes obtidos diretamente de corretoras dos Estados Unidos), bem como a metodologia usada para avaliar também foi completamente diferente.
Apesar disso, ele trazem uma observação interessante: o paper de Rama Cont foi lançado em 2001. Desde então, a regulação americana de compra e venda de ativos em bolsa mudou drasticamente (você avalie no Brasil). Por causa disso, é de certa forma natural que a dinâmica das negociações de ativos, e mesmo das flutuações, também tenha mudado, afetado em algum ponto o comportamento estatístico destas flutuações. Além disso, é importante considerar que a dinâmica do mercado de renda variável é fruto não só do seu contexto histórico mas também do comportamento e fator humano, que aliado às mudanças nas legislações, muda a forma de operação.
Epílogo
Foi muito curioso ver que uma simples análise não só levou a resultados em direções opostas às de um paper seminal, bem como ver que outro estudo conduzido de forma completamente diferente chegou à uma observação muito próxima. Este tipo de resultado tem um impacto adicional ainda, pois, no artigo de Cont, estes fatos estilizados também se configuram como propriedades das quais modelos que simulam a flutuação de preços de ativos deveriam ter. Como o tempo passou e a legislação mudou, vemos que realmente é necessário dar uma "reciclada" nestas propriedades. Além disso, é importante considerar que o artigo é de 2001 (23 anos atrás em relação ao tempo da escrita deste post). Em ciência, artigos com idade a partir de 5 anos já são considerados "antigos", sendo necessário estudar artigos mais recentes para checar as novidades. Por conta disso, é natural que conclusões obtidas há um bom tempo sejam refutadas/corrigidas/etc.
Conforme mencionei no início do post, os códigos e dados da análise estão disponíveis neste link, e para quem curte analisar dados, fica como dever de casa não só explorar essa análise desta vez considerando dados de intra-day, como também testar em outros ativos (ações individuais, outros ETFs etc.), bem como verificar se alguma volatilidade longa individual conseguiu ainda assim ter Informação Mútua melhor que alguma Volatilidade Curta. Outra coisa a se testar seria trocar a métrica de avaliação: ao invés de usar Informação Mútua, usar correlação, por exemplo.
Até a próxima postagem!